c++实现求最大公因数和最小公倍数

WIZ 自成一派 2023-09-05 21:03:47

Lv：45级

C++
#include<iostream>
using namespace std;
int GCD(int a,int b);
int LCM(int a,int b);
int main()
{
int num1,num2,gcd,lcm;
cout<<"求两个数的最大公约数及最小公倍数"<<endl<<endl;
cout<<"请输入两个数：";
cin>>num1>>num2;
gcd=GCD(num1,num2);
lcm=LCM(num1,num2);//输出最大公约数和最小公倍数
cout<<"最大公约数为："<<gcd<<endl;
cout<<"最小公倍数为："<<lcm<<endl;
system("pause");
return 0;
}
int GCD(int num1,int num2)
{
if(num1%num2==0)
return num2;
else return  GCD(num2,num1%num2);
}
int LCM(int a,int b)
{
int temp_lcm;
temp_lcm=a*b/GCD(a,b);//最小公倍数等于两数之积除以最大公约数
return temp_lcm;
}

• 

  WIZ 法师 #2

  2023-09-05 21:22:41

  
  用辗转相除法求最大公因数 

   辗转相除法的流程图如下：

  
  

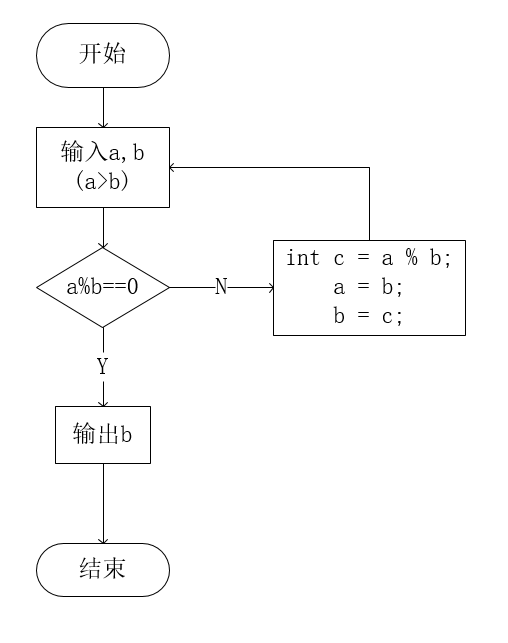
   其中，输入保证a>b。 参考代码如下：

  #include <iostream>
  using namespace std;
  
  int main(){<!-- -->
  int a, b;
  cin >> a >> b;
  // 假设确保 a > b
  while(a % b != 0){<!-- -->
  int c = a % b;
  a = b;
  b = c;
  }
  cout << b << endl;
  return 0;
  }

  特别的，如果能用头文件algorithm的话，可以直接使用__gcd(int a, int b)函数来算最小公因数。我用的dev-c++是可以跑的通的。
  参考代码如下：
  

  #include <iostream>
  #include <algorithm>
  using namespace std;
  
  int main(){
  	int a, b;
  	cin >> a >> b;
  	int n = __gcd(a, b);
  	cout << n << endl;
  	return 0;
  } 
  

  最小公倍数可以通过求得的最大公因数来计算。
  最小公倍数=a*b/最大公因数
  

  0 回复